渡辺先生が2023年3月で定年退官されて結構経ちますが，ホームページはまだ改修中です。
福井大学 工学部機械・システム工学科原子力安全工学コース，福井大学大学院 工学研究科安全社会基盤工学専攻原子力安全工学コース 熱水力研究室のホームページです。
当研究室では，原子炉内の熱流動に関する解析的・実験的研究を行っています。
詳細については右上のRESEARCHタブもしくはPAPERSタブをクリックしてください。
ツイニングプログラムというのがあり，ベトナムのハノイ工科大学から日本の参加大学に編入できるというシステムです。これに福井大も参加しており，集中講義に行ってきました。
担当は「熱力学」でした。日本に留学するのが目的のプログラムなので，学生さんは日本語の勉強をしていて，講義は日本語です。 月水金は4コマ（1コマ45分），火木は3コマで，合計5日間のわりと長めの集中講義です。
今週ずっとベトナムですが，先週の木金は筑波（製作中の実験装置の確認）にいってからのベトナムなので，結構大変です。。。
再来週はCFD4NRSで水戸です。。。
相変わらずのカオスな道路事情
大学構内
ベトナムのKFC。パスタとかまで売ってます。オリジナルチキンはいまいちでした。
小倉の原子力学会に来ました。 M1の和田さんがデータ同化の発表しました。最終日の最終セッションのわりに人がそれなりにいてくれて良かったです。
看板に予算を使ったみたいです。
金沢工業大学で第75回北陸流体工学研究会があって，データ同化について発表してきました。 北陸流体工学研究会は2回目なので，自己紹介的なつもりの発表でした。
初めての金沢。北陸新幹線速すぎて，敦賀から金沢で1時間かからないのは衝撃でした。
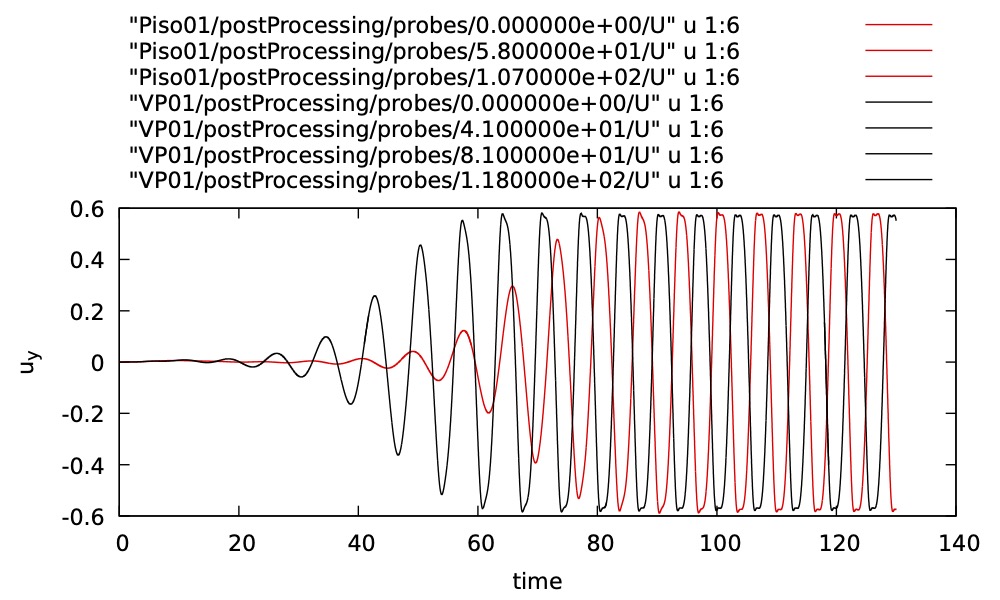
今回は角柱後流のカルマン渦の計算をVP法と通常の計算とで実施して，渦の放出周期が合うかやってみました。 完全に四角なので，一致するはず。
レイノルズ数は100です。
通常の計算（角柱部分のメッシュを設定）による流速分布
VP法による計算による流速分布
VP法のほうが不安定化（流れが振動しはじめて，渦が出るまで）が早いですが，最終的な渦の放出周期はほぼ一致しています。 （ここまで来るのに多少手間取ったりもしましたが。。。）
下図はスパン方向速度の時系列データです。赤が通常の計算，黒がVP法の計算によるものです。
ついでに渦度の動画
通常の計算（角柱部分のメッシュを設定）
VP法による計算
境界埋め込み法の1つであるVP法のコードをOpenFOAMに実装しました。実装したコードはこちら。 https://qiita.com/ishigaki/items/cfb20bc58c2ae6a633a0
境界適合格子でやったときとちゃんと比べてみました。NACA0012翼周りの流れをやります。
pisoFoam用のメッシュと，VP法つかったpisoFaomのvppisoFoam用のメッシュを作りました。blockMeshだけでほぼNACA0012通りの形状を再現できます。
メッシュ幅はおおよそ5mmです。
polyLineで翼表面の座標を直線で補間します。
/*--------------------------------*- C++ -*----------------------------------*\
| ========= | |
| \\ / F ield | OpenFOAM: The Open Source CFD Toolbox |
| \\ / O peration | Version: 2.3.1 |
| \\ / A nd | Web: www.OpenFOAM.org |
| \\/ M anipulation | |
\*---------------------------------------------------------------------------*/
FoamFile
{
version 2.0;
format ascii;
class dictionary;
object blockMeshDict;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
convertToMeters 1;
vertices
(
( -0.5 -1.25 -1 )
( -0.5 1.25 -1 )
( 0.3 -0.06001727 -1 )
( 0.3 0.06001727 -1 )
( 1.0089 -1.25 -1 )
( 1.0089 0 -1 )
( 1.0089 1.25 -1 )
( 3 -1.25 -1 )
( 3 0 -1 )
( 3 1.25 -1 )
( -0.5 -1.25 1 )
( -0.5 1.25 1 )
( 0.3 -0.06001727 1 )
( 0.3 0.06001727 1 )
( 1.0089 -1.25 1 )
( 1.0089 0 1 )
( 1.0089 1.25 1 )
( 3 -1.25 1 )
( 3 0 1 )
( 3 1.25 1 )
);
blocks
(
hex (0 2 3 1 10 12 13 11) (250 120 1) simpleGrading (1 1 1)
hex (0 4 5 2 10 14 15 12) (142 250 1) simpleGrading (1 1 1)
hex (3 5 6 1 13 15 16 11) (142 250 1) simpleGrading (1 1 1)
hex (4 7 8 5 14 17 18 15) (398 250 1) simpleGrading (1 1 1)
hex (5 8 9 6 15 18 19 16) (398 250 1) simpleGrading (1 1 1)
);
edges
(
polyLine 2 3 (
( 0.28 -0.05992581 -1 )
( 0.26 -0.059636853 -1 )
( 0.24 -0.059131171 -1 )
( 0.22 -0.058386276 -1 )
( 0.2 -0.05737543 -1 )
( 0.18 -0.056066189 -1 )
( 0.16 -0.054418208 -1 )
( 0.14 -0.052379745 -1 )
( 0.12 -0.049881816 -1 )
( 0.1 -0.046827704 -1 )
( 0.08 -0.043072299 -1 )
( 0.06 -0.03837581 -1 )
( 0.04 -0.032277225 -1 )
( 0.02 -0.023597771 -1 )
( 0.01 -0.017037074 -1 )
( 0.005 -0.012213147 -1 )
( 0 0 -1 )
( 0.005 0.012213147 -1 )
( 0.01 0.017037074 -1 )
( 0.02 0.023597771 -1 )
( 0.04 0.032277225 -1 )
( 0.06 0.03837581 -1 )
( 0.08 0.043072299 -1 )
( 0.1 0.046827704 -1 )
( 0.12 0.049881816 -1 )
( 0.14 0.052379745 -1 )
( 0.16 0.054418208 -1 )
( 0.18 0.056066189 -1 )
( 0.2 0.05737543 -1 )
( 0.22 0.058386276 -1 )
( 0.24 0.059131171 -1 )
( 0.26 0.059636853 -1 )
( 0.28 0.05992581 -1 )
)
polyLine 12 13 (
( 0.28 -0.05992581 1 )
( 0.26 -0.059636853 1 )
( 0.24 -0.059131171 1 )
( 0.22 -0.058386276 1 )
( 0.2 -0.05737543 1 )
( 0.18 -0.056066189 1 )
( 0.16 -0.054418208 1 )
( 0.14 -0.052379745 1 )
( 0.12 -0.049881816 1 )
( 0.1 -0.046827704 1 )
( 0.08 -0.043072299 1 )
( 0.06 -0.03837581 1 )
( 0.04 -0.032277225 1 )
( 0.02 -0.023597771 1 )
( 0.01 -0.017037074 1 )
( 0.005 -0.012213147 1 )
( 0 0 1 )
( 0.005 0.012213147 1 )
( 0.01 0.017037074 1 )
( 0.02 0.023597771 1 )
( 0.04 0.032277225 1 )
( 0.06 0.03837581 1 )
( 0.08 0.043072299 1 )
( 0.1 0.046827704 1 )
( 0.12 0.049881816 1 )
( 0.14 0.052379745 1 )
( 0.16 0.054418208 1 )
( 0.18 0.056066189 1 )
( 0.2 0.05737543 1 )
( 0.22 0.058386276 1 )
( 0.24 0.059131171 1 )
( 0.26 0.059636853 1 )
( 0.28 0.05992581 1 )
)
polyLine 3 5 (
( 0.32 0.05992788 -1 )
( 0.34 0.059672249 -1 )
( 0.36 0.059263278 -1 )
( 0.38 0.058712465 -1 )
( 0.4 0.058030108 -1 )
( 0.42 0.057225479 -1 )
( 0.44 0.056306948 -1 )
( 0.46 0.055282094 -1 )
( 0.48 0.054157786 -1 )
( 0.5 0.052940252 -1 )
( 0.52 0.051635135 -1 )
( 0.54 0.050247543 -1 )
( 0.56 0.048782083 -1 )
( 0.58 0.047242897 -1 )
( 0.6 0.045633691 -1 )
( 0.62 0.043957754 -1 )
( 0.64 0.042217983 -1 )
( 0.66 0.040416898 -1 )
( 0.68 0.038556656 -1 )
( 0.7 0.036639067 -1 )
( 0.72 0.034665604 -1 )
( 0.74 0.032637411 -1 )
( 0.76 0.030555316 -1 )
( 0.78 0.028419835 -1 )
( 0.8 0.02623118 -1 )
( 0.82 0.023989265 -1 )
( 0.84 0.021693713 -1 )
( 0.86 0.019343859 -1 )
( 0.88 0.016938755 -1 )
( 0.9 0.014477173 -1 )
( 0.92 0.011957609 -1 )
( 0.94 0.009378289 -1 )
( 0.96 0.006737166 -1 )
( 0.98 0.004031929 -1 )
( 1 0.00126 -1 )
)
polyLine 2 5 (
( 0.32 -0.05992788 -1 )
( 0.34 -0.059672249 -1 )
( 0.36 -0.059263278 -1 )
( 0.38 -0.058712465 -1 )
( 0.4 -0.058030108 -1 )
( 0.42 -0.057225479 -1 )
( 0.44 -0.056306948 -1 )
( 0.46 -0.055282094 -1 )
( 0.48 -0.054157786 -1 )
( 0.5 -0.052940252 -1 )
( 0.52 -0.051635135 -1 )
( 0.54 -0.050247543 -1 )
( 0.56 -0.048782083 -1 )
( 0.58 -0.047242897 -1 )
( 0.6 -0.045633691 -1 )
( 0.62 -0.043957754 -1 )
( 0.64 -0.042217983 -1 )
( 0.66 -0.040416898 -1 )
( 0.68 -0.038556656 -1 )
( 0.7 -0.036639067 -1 )
( 0.72 -0.034665604 -1 )
( 0.74 -0.032637411 -1 )
( 0.76 -0.030555316 -1 )
( 0.78 -0.028419835 -1 )
( 0.8 -0.02623118 -1 )
( 0.82 -0.023989265 -1 )
( 0.84 -0.021693713 -1 )
( 0.86 -0.019343859 -1 )
( 0.88 -0.016938755 -1 )
( 0.9 -0.014477173 -1 )
( 0.92 -0.011957609 -1 )
( 0.94 -0.009378289 -1 )
( 0.96 -0.006737166 -1 )
( 0.98 -0.004031929 -1 )
( 1 -0.00126 -1 )
)
polyLine 13 15 (
( 0.32 0.05992788 1 )
( 0.34 0.059672249 1 )
( 0.36 0.059263278 1 )
( 0.38 0.058712465 1 )
( 0.4 0.058030108 1 )
( 0.42 0.057225479 1 )
( 0.44 0.056306948 1 )
( 0.46 0.055282094 1 )
( 0.48 0.054157786 1 )
( 0.5 0.052940252 1 )
( 0.52 0.051635135 1 )
( 0.54 0.050247543 1 )
( 0.56 0.048782083 1 )
( 0.58 0.047242897 1 )
( 0.6 0.045633691 1 )
( 0.62 0.043957754 1 )
( 0.64 0.042217983 1 )
( 0.66 0.040416898 1 )
( 0.68 0.038556656 1 )
( 0.7 0.036639067 1 )
( 0.72 0.034665604 1 )
( 0.74 0.032637411 1 )
( 0.76 0.030555316 1 )
( 0.78 0.028419835 1 )
( 0.8 0.02623118 1 )
( 0.82 0.023989265 1 )
( 0.84 0.021693713 1 )
( 0.86 0.019343859 1 )
( 0.88 0.016938755 1 )
( 0.9 0.014477173 1 )
( 0.92 0.011957609 1 )
( 0.94 0.009378289 1 )
( 0.96 0.006737166 1 )
( 0.98 0.004031929 1 )
( 1 0.00126 1 )
)
polyLine 12 15 (
( 0.32 -0.05992788 1 )
( 0.34 -0.059672249 1 )
( 0.36 -0.059263278 1 )
( 0.38 -0.058712465 1 )
( 0.4 -0.058030108 1 )
( 0.42 -0.057225479 1 )
( 0.44 -0.056306948 1 )
( 0.46 -0.055282094 1 )
( 0.48 -0.054157786 1 )
( 0.5 -0.052940252 1 )
( 0.52 -0.051635135 1 )
( 0.54 -0.050247543 1 )
( 0.56 -0.048782083 1 )
( 0.58 -0.047242897 1 )
( 0.6 -0.045633691 1 )
( 0.62 -0.043957754 1 )
( 0.64 -0.042217983 1 )
( 0.66 -0.040416898 1 )
( 0.68 -0.038556656 1 )
( 0.7 -0.036639067 1 )
( 0.72 -0.034665604 1 )
( 0.74 -0.032637411 1 )
( 0.76 -0.030555316 1 )
( 0.78 -0.028419835 1 )
( 0.8 -0.02623118 1 )
( 0.82 -0.023989265 1 )
( 0.84 -0.021693713 1 )
( 0.86 -0.019343859 1 )
( 0.88 -0.016938755 1 )
( 0.9 -0.014477173 1 )
( 0.92 -0.011957609 1 )
( 0.94 -0.009378289 1 )
( 0.96 -0.006737166 1 )
( 0.98 -0.004031929 1 )
( 1 -0.00126 1 )
)
);
boundary
(
inlet
{
type patch;
faces
(
(0 1 11 10)
);
}
outlet
{
type patch;
faces
(
(0 4 14 10)
( 4 7 17 14)
(1 6 16 11)
(6 9 19 16)
(7 8 18 17)
(8 9 19 18)
);
}
airfoil
{
type wall;
faces
(
(2 5 15 12)
(2 3 13 12)
(3 5 15 13)
);
}
front
{
type empty;
faces
(
(0 2 3 1)
(0 4 5 2)
(3 5 6 1)
(4 7 8 5)
(5 8 9 6)
(10 12 13 11)
(10 14 15 12)
(13 15 16 11)
(14 17 18 15)
(15 18 19 16)
);
}
);
mergePatchPairs
(
);
// ************************************************************************* //
研究室配属前の学生さんが研究の初歩みたいなことをやるという制度が最近できました。
その一環として，2年生・3年生の希望学生に対して，プログラムを教えるというのをやりました。うちの研究室だと計算がメインにはなるので，その第一歩です。
2024年に，PythonとかJuliaとかを教えるというのをやってて，まずはちゃんとコンパイルする言語を勉強したほうがいいように思い始めたので，原点に立ちかえって，Fortranやりました。大規模計算とかだとFortranはまだまだ現役というかメインストリームなので，Fortranです。
原子力安全工学コースには副専攻卒研という制度があるので，他学科・他コースからでも卒業研究できます。他学科，他コースの人でも歓迎します。 今回はプログラムの勉強会でしたが，ぼちぼち進めるので研究室留学に興味あったら連絡ください。
2024年9月にあった若手フォーラムでの山下さんの発表「格納容器雰囲気の熱流動に対する輻射伝熱モデルの影響評価」が若手交流フォーラム優秀発表賞に選ばれました。 おめでとうございます。
輻射伝熱の解析で修論発表を行い，優秀論文賞を受賞しました。おめでとう。
シビアアクシデント時における格納容器内熱水力挙動の解析に用いられる凝縮モデルにはおおよそ2種類あります。1つは実験相関式で凝縮量を与えるモデルで，もう1つは非凝縮ガス中における水蒸気の物質拡散量から凝縮量を求めるモデルです。
2つ目の物質拡散量から凝縮量を求めるモデルを用いて，解析を行っています。そのモデルの解釈についてメモ書きを作成しました。 論文にするほどでもないので，ここで公開します。
このサイトはhugoで書いた文章をHTMLに変換して作っています。
hugoのv0.122からLaTeXの数式を変換できるようになりました。
参照 https://text.baldanders.info/remark/2024/01/tex-math-expression-in-hugo-0_122/
割と簡単に数式がかけます。\labelとかは使えないみたいですが。。。
\[ \begin{aligned} & \frac{\partial \rho}{\partial t} + \frac{\partial}{\partial x_i}(\rho u_i) = 0 \\ & \frac{\partial \rho u_j}{\partial t} + \frac{\partial}{\partial x_i}(\rho u_i u_j) = -\frac{\partial p}{\partial x_j} + \frac{\partial \tau_{ij}}{\partial x_i}\\ & \frac{\partial \rho e}{\partial t} + \frac{\partial}{\partial x_i}(\rho u_i e) = \frac{\partial}{\partial x_i}\left(k\frac{\partial T}{\partial x_i}\right) - \frac{\partial}{\partial x_i}(pu_i) + \frac{\partial}{\partial x_i}(u_j \tau_{ij}) \end{aligned} \]